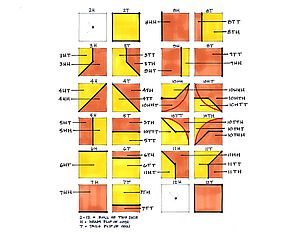
The Drawings
Chance Drawing #1
-Three square grids each with 15 modules on a side (225 total) are placed one over the other and offset by 1-1/8”, vertically and horizontally.
-The alphabet is applied to each grid
-A different color is added to each grid with ochre added to the bottom grid which is superimposed by the green grid then, in turn, superimposed by the teal grid.
-An arbitrary black band of graphite passes from left to right under all three grids and then rising to obscure each grid in succession.
-Total amount of information includes 675 modules.
Chance Drawing #2
-A four way symmetrical grid has diminishing module sizes as they move to the center of the drawing.
-The grid diminishes in square module sizes from the perimeter to the center as follows: 6” x 6” grid modules surround 3” modules which surround 1-1/2” modules, then 1”, ¾” and finally ½” x ½” grid modules.
-The alphabet is applied to the grid starting with side #1 at the bottom, then rotated 90 degrees with side #2 on the bottom and applied again until there are four grids of alphabet superimposed on each other.
-Total amount of information includes 2,032 modules.
Chance Drawing #3
-Two square grids each with 15 modules on a side (224 total) are placed one over the other and offset by 1-1/8” vertically and horizontally.
-Sides of one module deep grids connect the two larger grids forming a three dimensional, rather flat, rectangular box.
-The alphabet is applied to the grids on all six sides.
-Color is added with dark blue applied to each grid module on the front three sides, and light blue applied to each grid module on the back three sides.
-An arbitrary black shape of graphite passes from left to right under the box then rising vertically to obscure more and more modules.
-Total amount of information includes 510 modules.
Chance Drawing #4
-A cylindrical grid 10 modules high and 29 modules in circumference is placed against a background grid of the same module size and also 10 modules high which runs off the drawing area left and right.
-The alphabet is applied to both grids.
-Color is added with dark red to the exterior surface modules of the cylinder and light red to the inner surface modules of the cylinder. A darker red is added to the flat background grid.
-An arbitrarily chosen yellow cylinder contains elongated or stretched alphabet marks.
-Total amount of information includes 470 modules.
Chance Drawing #5
-A cube is projected so that all sides and all modules have the same dimensions. All six sides are drawn as a grid of 15 x 15 modules (225 total on each side of the cube).
-The alphabet is applied to each grid module on all six sides.
-Total amount of information includes 1,350 modules.
Chance Drawing #6
-Two grids of partial cylindrical shape are placed, one with a smaller radius inside the other, each with a surface of 11 modules x 11 modules (121 total).
-The two surfaces are connected on all four sides by grids two modules deep.
-All six sides of the partial cylinder are shown.
-The alphabet is applied to each grid module.
-Color is added with dark red as the inner cylindrical surface, light red as the outer cylindrical surface and medium red on the sides joining the two curved surfaces.
-Total amount of information includes 330 modules.
Chance Drawing #7
-Six grids, 10 modules wide x approximately 18 modules long (in the long dimension the grids run off the drawing surface) are superimposed one above the other.
-Each grid is projected at a different angle, but all modules have the same dimensions.
-The six grids are organized somewhat like pages in a book open about its spine.
-The alphabet is applied to each grid module with color added arbitrarily as a free-hand lines and points in black, green or purple.
-Total amount of information includes 1,080 modules.
Chance Drawing #8
-Two grids are drawn as mirror image perspective planes facing each other, each 15 modules high x 10 modules wide. Dimensions vary as the perspective vanishes.
-The alphabet is applied to each grid module.
-Each module in each horizontal row of modules in the left or right grid may or may not have a mirror image match in the same row of modules in the opposing grid.
-If a mirror symmetry is found, all end points of both mirrored module letters are connected by lines spanning the separation between the two grids.
-Total amount of information includes 300 modules
-Total amount of information also includes 53 mirror image connections.
Chance Drawing #9
-Five geometric volumes are superimposed. Each volume is drawn with grids on all sides of the particular shape. One is in perspective with diminishing module sizes (the gold rectangular volume) and the other four are volumes without perspective vanishing points
-The alphabet is applied to each module.
-Color is applied arbitrarily to each volume on its grid modules.
-The volumes contain the following number of modules:
-The gold rectangular volume is 10 x 10 x 2 modules = 280 total.
-The purple rectangular volume is 27 x 6 x 1 modules = 390 total.
-The red partial cylinder volume is 10 x 10 x 1 modules = 240 total.
-The yellow cylinder volume is 5 modules in circumference x approximately 23 modules = 115 total.
-The blue prism volume is 6 modules x approximately 26 long x 3 sides = 468 total.
-Total amount of information includes 1,493 modules.
Chance Drawing #10
-Three square grids each with 15 modules on a side (225 total) are place one over the other and each is offset from the next, vertically and horizontally by 1-1/4”.
-The middle grid is the main grid; the grid to the lower left is the T (tails) grid and the grid to the upper right is the H (heads) grid.
-The alphabet is first applied to the main grid modules.
-A coin is then flipped to determine whether the T grid or the H grid receives the alphabet in its module corresponding to that in the main grid. If the H grid module is filled, the T grid module is left blank and so on. This continues through 225 coin flips.
-A coin is then flipped again for each empty module whether it is in the H or the T grid. If a module in the H grid is presently filled and another H is flipped, the same letter is repeated in the T grid module. Similarly, if a module in the T grid is filled and another T is flipped the same letter is repeated in the H grid module.
-However, if on the second flip, a T follows an H or an H follows a T, no alphabet letter is added to the empty module in the third grid.
-This process results in a random number of two and three module units. In each unit, all end points of the alphabet lines are connected by lines point to point.
-Color is applied arbitrarily to the new shapes: light yellow to a two-module combination and dark yellow to a three-module combination.
-Total amount of information includes 675 modules.
-Total amount of information also includes 100 two-module units (light yellow)
-Total amount of information also includes 125 three-module units (dark yellow).
Typical notebook page listing dice tosses followed by coin flips
-This list of randomly generated number and letter combinations is used as a guide for applying ‘letters’ or lines to the grid modules on a chance drawing. These number-letter combinations can also be considered as names for the letters.
-The order in which the list must be used can be sequentially left to right/top to bottom, or right to left/bottom to top. It can also be used starting at any point in the entire list, going forward or backward sequentially.
-Following the entries in the list, the alphabet lines are then applied sequentially to the modules of the grids, either horizontally or vertically, module by module and row by row, but always following a repetitive, orderly progression.
-Note that no identification of color application is found in this list. The arbitrary decision of whether or not to add color comes after the grids are filled.
-The notebook contains 3,087 entries.
The alphabet of lines with color added
-More information can be added to each module by the application of color to it as shown in this modified alphabet.
-Another coin is flipped for each ‘letter’ and heads or tails indicates where the color is to be applied.
-Color is only added once to a module and the choice of a hue is arbitrary.
-A coin flip of a heads means the color may only be applied above or to the right of the line in the module.
-A flip of a tails means the color may only be applied below or to the left of the line in the module.
Special cases include:
-A 2H or a 12H never has color added to its module.
-A 12H or a 12T always has color added, filling the module, without the need to flip a coin.
-If a heads comes up for a 4H or a 4T, the color is always applied to the lower right or upper right of the diagonal line. If a tails comes up for a 4H or 4T, the color is always applied to the lower left or the upper left of the diagonal line.
-If a line is found on one edge of a module and a flip of a heads or tails would place the color outside of the module, color is not added. For example, an 8H has a vertical line on the left hand edge of the module. If a T is rolled, no color is added.
-If an H is rolled, color is added to the right of the line, filling the module.
-Adding color gives any ‘letter’ a new name. For example a 5H with an H added for color becomes a 5HH; a 5H with a T added for color becomes a 5HT.
These drawings gave me, at least partially, the opportunity to work with chance as part of the process of making a drawing. It meant giving up control over some of the visual results. The inspiration came first from reading I have been doing in certain areas of theoretical physics. In particular, it came from my interest in the quantum world where events can only be understood and determined by probability. Nothing is certain in the world of small particles. A single electron can be in many places at the same time and take many simultaneous paths from A to B. Only when it is observed by experiment does it land in a specific place. Even then it is never stationary. We cannot control events as they unfold in the micro scale of the quantum world; at best we can only make predictions about probable outcomes.
Back in the macro world, it is refreshing to give up a certain amount of control in making art. But, there are also many arbitrary and subjective choices I made in the drawings of this series. A general description of the process of making these drawings will demonstrate the various moments where I kept control of a visual result, or not.
I began with a group of 28 line configurations including two points. This group is my alphabet of marks or more metaphorically, ‘letters’. Each represents a roll of two dice followed by a flip of a coin. One line may represent a roll of a 7 followed by a flip of heads (7H), a different type of line represents a roll of a 3 followed by a flip of tails (3T) and so on. These designations are the names for the letters of my alphabet. Each of these designated marks relates to the others in being able to be placed in a square, a module, of the same dimension.
I then compiled a randomly generated master list of dice rolls and coin flips, 2T, 6H, 11T, 10HT, and so on. These are kept in a notebook. There are presently 3,087 entries.
To control where these lines may be placed in a drawing, I arbitrarily created grids of lines that may be flat and square, but also diminishing in perspective, curved or combined to form three-dimensional volumes. These planes, or membranes, are placed on the drawing following a visual idea or concept of my choosing.
Next, I filled the grids with the letters of my line alphabet; each module in the grid received a letter. To do this I used the master list. I can proceed forward or backward with the list and start at any point in it, but I follow whatever order is there with out skipping an entry or jumping ahead. The grids are filled in an orderly process, for example either left/right or right/left by columns and top/down or bottom/up by rows. So, the lines and points are applied with no immediate control over what letter follows another as the alphabet is placed in the modules of the grid.
Once the grid or grids are filled, the drawing is complete or a decision is then made to introduce color. Color is added by a process of again flipping a coin which determines where in a given module of the grid the color is placed, left or right of a vertical line, above or below a horizontal line. The choice of color is subjective and arbitrary.
Finally, in some of the drawings another very subjective decision might be made about the drawing as a visual whole. Graphite might be added to obscure parts of grids or their relationship to each other. Lines or color might be added to create additional connections between letters in adjacent grids. These decisions might in turn lead to more coin flipping, another layer of chance input.
I have mentioned my interest in theoretical physics leading to the incorporation of chance in this work. There is also a particular idea that I’ve seen in reference to Information Theory and Black Hole Theory that has informed this series. It is called the Holographic Principle and it has influenced Chance Drawings #5, #6 and #9. In my own words, the principle suggests that the total amount of information that a given volume can contain is limited by the number of Planck bits or units on the surface of an envelope containing that volume. A Planck unit is very small and perhaps the smallest area that can exist in our universe (it is 10 to the minus 33 centimeters on a side). In any case, the grids that combine to envelope volumes in some of the drawings do contain their information in bits, in the letters and colors within the modules. There is a hierarchy of information in the drawings.
Another inspiration from theoretical physics is seen in Chance Drawing #8. A cosmological concept that has emerged from String Theory posits that the origin of our particular universe came about by the collision of two membranes floating in a more infinite and more ancient universe than our own. Furthermore, the smallest particles of our presumed reality are thought to be strings and loops of energy that belong on these membranes and may move between them. I think of the grids found in these drawings as membranes containing information and that the membranes commute with each other.
In a gesture of full disclosure, I admit that the process of giving up control to chance and random acts was surprisingly difficult at times. After flipping 10 tails in a row, I found myself desperately wanting a heads. When following the master list and adding letters to the grids I became at times visually frustrated by the repetition of certain kinds of lines or points. I was often unhappy with the way color was accumulating. I even cheated on myself once in a while, maybe skipped an entry in my grand list or giving myself a second chance on a coin flip! I find the relationship between art and personal control quite complex.
Ultimately, however, I’m interested in the information which these drawings contain and where it comes from. Bits of information are presented in the form of symbols - lines and points - that in turn represent acts of chance. These symbolic bits are integrated into the drawing via various random processes. Subjective free will is added at stages in the process of creating a drawing that communicates an idea. The final and total amount of information in the drawings includes chance and free will, giving up control and asserting it.